Ultimate Guide to Coherence Time: Everything You Need to Know
2025.05.16 · Blog coherence time
In the world of quantum computing, coherence time is one of the most critical parameters determining the performance and reliability of a quantum computer. It directly impacts how long a quantum bit (qubit) can maintain its quantum state, which is essential for performing accurate quantum computations.
In this post, we'll explain what coherence time is, why it matters, what factors influence it, and how it's measured and improved across various quantum technologies.

What is Quantum Coherence?
Quantum coherence describes the ability of a quantum system (like a qubit) to exist in a superposition of states. Unlike classical bits that are either 0 or 1, qubits can be in a combination of both simultaneously. This delicate state allows quantum computers to perform computations in parallel. However, interactions with the environment cause decoherence, which destroys this superposition.
What Is Coherence Time?
Coherence time refers to the duration over which a qubit retains its quantum properties — specifically, superposition and entanglement — before it loses them due to interaction with the environment (a process called decoherence).
In physics terms, coherence time is studied using the theory of open quantum systems and the density matrix formalism.
There are generally two types of coherence time:
-
T1 (relaxation time): The time it takes for a qubit to lose energy and fall from the excited state to the ground state.
-
T2 (dephasing time): The time over which the phase information of the qubit's wavefunction is preserved.
T2 is always less than or equal to 2*T1.
T1 vs. T2: What's the Difference?
T1 and T2 represent different types of quantum noise:
-
T1 affects the energy state (population decay).
-
T2 affects the phase coherence (loss of interference).
T1 measures energy loss, and T2 measures how long the qubit maintains phase coherence. Understanding both is critical, as they impact gate operations, measurement accuracy, and the ability to perform quantum error correction.
Why Is Coherence Time Important?
A longer coherence time means:
-
More quantum operations can be performed before errors occur.
-
Higher fidelity in quantum gates.
-
Improved error correction, as more reliable data can be captured before the system decoheres.
-
Better scalability, because qubits with longer coherence are more suitable for large-scale quantum algorithms.
In short, coherence time defines the "lifetime" of usable quantum information. If a qubit decoheres too quickly, computations become unreliable or completely fail.
What Affects Coherence Time?
Several factors influence coherence time in quantum computing. These factors vary depending on the type of qubit but generally fall into three broad categories: environmental noise, material imperfections, and control system limitations.
Here's a breakdown:
1. Environmental noise: Fluctuations in magnetic or electric fields can disturb qubits.
2. Qubit material and architecture: Superconducting qubits, trapped ions, spin qubits, and photonic qubits each have different decoherence sources.
|
Qubit Type |
Limiting Factors |
|
Superconducting |
Dielectric and flux noise, TLS, charge noise |
|
Trapped Ion |
Magnetic field drift, laser fluctuations, motional heating |
|
Spin Qubits |
Hyperfine interactions, charge trap noise |
|
Photonic Qubits |
Minimal decoherence in transit, but poor memory |
|
Neutral Atoms |
Laser intensity noise, vacuum fluctuations |
3. Temperature: Quantum computers often operate at cryogenic temperatures to reduce thermal noise.
4. Control precision: Poor control electronics can introduce noise and errors that shorten coherence.
For instance, trapped-ion qubits can have T2 times lasting seconds or more, while superconducting qubits typically have coherence times in the microsecond to millisecond range.
How Is Coherence Time Measured?
Coherence time in quantum computing is measured through specialized experimental techniques that reveal how long a qubit maintains its quantum state before decohering. The two main types of coherence time — T₁ (relaxation time) and T₂ (dephasing time) — are measured differently:
T₁ Measurement (Energy Relaxation Time)
Goal: Measure how long a qubit stays in an excited state before relaxing to the ground state.
Procedure:
1. Excite the qubit to the |1⟩ state using a microwave pulse.
2. Wait for a variable delay time (τ).
3. Measure the state of the qubit.
4. Repeat for different delay times to gather decay statistics.
Result: The probability of finding the qubit in |1⟩ decays exponentially with time:
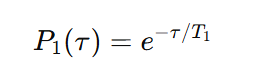
T₁ is extracted by fitting this decay curve.
T₂ Measurement (Phase Coherence Time)
T₂ measures how long the phase of a superposition state is preserved.
Method 1: Ramsey Interferometry
Steps:
1. Apply a π/2 pulse to put the qubit in a superposition.
2. Let it evolve freely for time τ.
3. Apply another π/2 pulse.
4. Measure the final state.
5. Vary τ to observe oscillations.
Result: The oscillation amplitude decays over time due to phase noise. T₂* is obtained from the decay envelope.
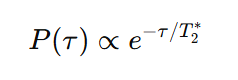
Method 2: Spin Echo (Hahn Echo)
Steps:
1. π/2 pulse → free evolution (τ/2) → π pulse → free evolution (τ/2) → π/2 pulse.
2. The π pulse refocuses slow noise, extending coherence time.
3. The decay of signal gives the T₂ (echo) time, typically longer than T₂*.
Method 3: CPMG Sequences
1. Extends the spin echo by applying multiple π pulses.
2. Filters out different types of noise to probe the noise spectrum more deeply.
3. Provides a more robust estimate of usable coherence under realistic conditions.
Summary:
|
Method |
Measures |
Noise Sensitivity |
Notes |
|
T₁ Measurement |
T₁ |
Amplitude noise |
Energy relaxation decay |
|
Ramsey |
T₂* |
Fast phase noise |
Basic phase decoherence |
|
Spin Echo |
T₂ |
Slow phase noise |
Corrects for low-frequency drift |
|
CPMG |
Extended T₂ |
Tailored noise rejection |
High-precision coherence control |
These measurements are crucial for characterizing qubit quality, optimizing control pulses, and determining feasibility for error-corrected quantum computing.
Coherence Time in Different Qubit Technologies
|
Qubit Type |
T1/T2 Range |
|
Superconducting Qubits |
50–300 µs (T1), 50–200 µs (T2) |
|
Trapped Ions |
Up to 10 seconds or more |
|
Photonic Qubits |
Virtually unlimited (no memory) |
|
Spin Qubits |
~ms to seconds (in isotopically pure silicon) |
These values evolve rapidly with quantum research and improved engineering.
How to Improve Coherence Time?
Improving coherence time is a critical step toward building scalable, fault-tolerant quantum computers. The longer a qubit retains its quantum state, the more reliable quantum operations become. Below are the most effective techniques to enhance coherence time, categorized by approach:
1. Better Materials Engineering
Use High-Purity Materials
-
Eliminate impurities and isotopic variations that act as sources of noise.
-
Example: Use isotopically pure silicon-28 (^28Si) in spin qubits to remove nuclear spin noise.
Reduce Dielectric Losses
-
In superconducting qubits, interface and bulk materials can contain two-level systems (TLS) that cause energy loss.
-
Improving the oxide layers and using low-loss substrates like sapphire or silicon helps mitigate this.
Surface Treatment and Passivation
-
Proper cleaning and surface coating (e.g., hydrophobic layers) reduce defects and unwanted charge traps.
2. Environmental Isolation
Cryogenic Cooling
-
Lowering temperature (to ~10 mK in dilution refrigerators) suppresses thermal excitations that can cause decoherence.
Magnetic and Electromagnetic Shielding
-
Shielding the quantum system from ambient magnetic fields and radio-frequency (RF) interference preserves coherence.
Vacuum Chambers
-
For trapped-ion and neutral atom qubits, ultra-high vacuum is essential to avoid collisions with residual gas molecules.
3. Improved Control and Calibration
Stable Microwave and Laser Sources
-
Quantum gates rely on precise frequency and phase; using ultra-stable sources reduces dephasing.
Calibrated Pulse Shaping
-
Use Gaussian, DRAG, or machine-learned pulse shapes to reduce leakage errors and minimize decoherence.
Active Feedback and Drift Compensation
-
Regular recalibration or real-time feedback corrects for slow drift in qubit frequency or amplitude response.
4. Dynamical Decoupling Techniques
These are control-pulse sequences that "average out" certain noise sources by flipping the qubit's state periodically.
Common Schemes:
-
Spin Echo (Hahn Echo)
-
Carr–Purcell–Meiboom–Gill (CPMG)
-
Uhrig Dynamical Decoupling (UDD)
These techniques extend coherence by canceling the effects of slow noise fluctuations.
5. Qubit Design Optimization
Use Robust Qubit Architectures
-
Designs like the transmon qubit reduce sensitivity to charge noise.
-
Fluxonium and cat qubits are newer designs aimed at achieving longer T₁ and T₂.
3D Qubits
-
Encasing qubits in three-dimensional cavities (vs planar layouts) helps isolate them from surface defects and reduces participation in lossy materials.
Topological Qubits (Future-Oriented)
-
These hypothetical qubits store quantum information non-locally, making them inherently protected against local decoherence.
6. Better Qubit Connectivity and Crosstalk Reduction
-
Minimize Qubit Coupling Crosstalk: Isolate control lines and optimize layout to prevent operations on one qubit from affecting others.
-
Use Tunable Couplers: Dynamically adjust inter-qubit interactions to turn off unwanted crosstalk.
Top quantum computing companies like Google, IBM, and SpinQ are actively exploring new materials, error mitigation techniques, and hardware designs to extend coherence times.
How Coherence Time Impacts Real-World Quantum Applications
Coherence time plays a critical role in determining what quantum systems can achieve in practice:
-
Quantum chemistry simulations: Require long coherence to preserve entangled states during complex, multi-step calculations.
-
Quantum optimization algorithms: Rely on deep circuits that must finish before decoherence occurs.
-
Quantum communication: Quantum memories need extended coherence to enable entanglement distribution and reliable synchronization across quantum networks.
Final Thoughts
Coherence time is a fundamental factor in the race toward practical quantum computing. It determines how long qubits can function effectively, shaping the limits of quantum algorithms and real-world applications. As the field advances, improving coherence time remains a top priority to unlock the full potential of quantum machines.
FAQs
What is a good coherence time?
A good coherence time depends on the qubit type, but typically, anything above 100 microseconds is considered strong for superconducting qubits. For trapped ions, coherence times can reach seconds or more.
Can coherence time be infinite?
In theory, no. All physical systems interact with their environment, so some decoherence is inevitable. However, certain techniques (like quantum error correction or topological qubits) aim to make effective coherence times arbitrarily long.
How does temperature affect coherence?
Higher temperatures introduce thermal noise, which disrupts quantum states and shortens coherence time. That's why most quantum computers operate at cryogenic temperatures close to absolute zero.
Why is coherence time important for quantum circuit depth?
Quantum algorithms consist of sequences of logic gates. The circuit depth must be shorter than the coherence time, or the qubit will decohere mid-computation. This limits the complexity of algorithms on near-term devices and motivates the use of error mitigation and quantum error correction.
Does longer coherence time mean better gate fidelity?
Long coherence time doesn't always mean high gate fidelity. While coherence time determines how long a qubit can survive, gate fidelity measures how accurately we can manipulate it. Both metrics are essential for evaluating qubit quality and reliability.
Featured Content






