Density Matrix Explained: Quantum States Made Clear
2025.05.16 · Blog density matrix
Density Matrix: The Ultimate Guide to Quantum States
In the classical world, we're used to certainty—particles have definite positions and velocities. But in quantum mechanics, the story is far richer. Enter the density matrix, a powerful mathematical tool that allows us to describe both pure and mixed quantum states, providing insight into everything from quantum decoherence to quantum computing.
Whether you're a student, researcher, or quantum enthusiast, this guide will walk you through the fundamentals, applications, and significance of the density matrix in modern physics.
What Is a Density Matrix?
In quantum mechanics, a system's state is typically represented by a wavefunction ∣ψ⟩. However, this only works when the system is in a pure state—a complete, well-defined quantum state.
But what if the system is in a statistical mixture of states, like a qubit that has a 50% chance of being in ∣0⟩ and 50% in∣1⟩? The wavefunction doesn't suffice. That's where the density matrix (or density operator) comes in.
Definition:
The density matrix ρ is defined as:
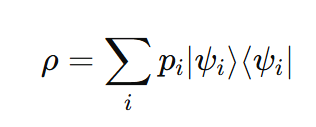
Here:
-
pi is the probability of the system being in state ∣ψi⟩
-
The sum runs over all possible states
-
ρ is a positive semi-definite, Hermitian operator with trace = 1
Pure vs Mixed States
Pure State:
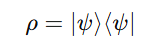
-
Represents complete knowledge of the system
-
Tr(ρ2)=1
Mixed State:
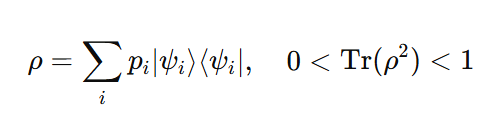
-
Represents incomplete knowledge (a statistical ensemble)
This distinction is crucial in quantum computing and quantum information, where noise and environment lead to mixed states due to decoherence.
Key Properties of the Density Matrix
-
Hermitian: ρ=ρ†
-
Trace is One: Tr(ρ)=1
-
Positive Semi-definite: All eigenvalues ≥0
-
Supports Expectation Values:
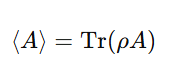
for any observable A
Why Density Matrices Matter in Quantum Computing
In real-world quantum computers:
-
Noise corrupts quantum states
-
Entanglement creates complex joint states
-
Partial measurements leave systems in mixed states
The density matrix provides a complete description of these scenarios.
Use Cases:
-
Quantum error correction: Track errors statistically
-
Quantum algorithms: Analyze decohered systems
-
Quantum communication: Evaluate entanglement and fidelity
Reduced Density Matrix and Entanglement
If you have a composite system A⊗B, and you only care about part A, you can trace out system B:
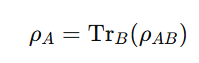
This partial trace gives a reduced density matrix, which is central to analyzing entangled states and subsystem dynamics.
Bloch Sphere and Qubits
For a single qubit, the density matrix can be visualized using the Bloch sphere. Any qubit state (pure or mixed) maps to a point inside the unit sphere:
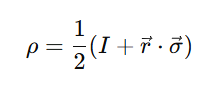
Here, r is the Bloch vector, and σ is the vector of Pauli matrices. Pure states lie on the surface, mixed ones inside.
Conclusion: A Tool Beyond Wavefunctions
The density matrix framework is essential for modern quantum physics. It extends the power of wavefunctions, enabling physicists and engineers to model realistic, noisy, or entangled systems.
If you're diving into quantum computing, mastering the density matrix isn't optional—it's foundational.
Featured Content






