Bloch Sphere Explained: Qubit Visualization Made Simple

The Mathematics Behind the Bloch Sphere

A qubit, the basic unit of quantum information, is described by a linear combination of basis states:

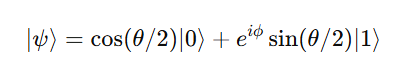
This formula defines a point on the unit sphere using two angles:

• θ (theta): angle from the Z-axis
• φ (phi): angle in the X-Y plane

These parameters map to a 3D vector, known as the Bloch vector:

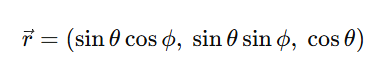
The result? Any pure qubit state corresponds to a unique point on the sphere's surface.

 

 

How the Bloch Sphere Differs from Classical Bit Models

In classical computing, a bit can only exist in one of two states: 0 or 1. These are discrete and mutually exclusive. In contrast, a quantum bit (qubit) can exist in a superposition of both |0⟩ and |1⟩ simultaneously.

The Bloch Sphere represents this difference visually:

• Every point on the surface of the Bloch Sphere corresponds to a pure qubit state, described by continuous parameters θ and φ.
• Unlike classical bits that "jump" between 0 and 1, qubits transition smoothly between states via quantum operations.
• The north and south poles represent the classical states |0⟩ and |1⟩, but the entire sphere surface embodies the quantum realm of infinite superpositions.

This geometric interpretation emphasizes the continuity and complexity of quantum information compared to classical binary logic.

Why the Bloch Sphere Matters in Quantum Computing

The Bloch Sphere is not just a visualization—it's a vital tool for:

Understanding Superposition: A qubit can exist in both |0⟩ and |1⟩ states simultaneously. The sphere helps visualize this as a point between the poles.

Explaining Quantum Gates: Quantum gates like X, Y, and Z correspond to rotations around the sphere's axes. The Bloch Sphere makes gate effects intuitive.

Visualizing Phase and Interference: The relative phase of a quantum state is shown as rotation around the vertical axis, which is otherwise invisible in classical bits.

Teaching and Debugging Quantum Algorithms: Tools like IBM Qiskit and Bloch sphere simulators often show Bloch vectors to help developers understand quantum behavior.

Quantum Gates as Rotations on the Bloch Sphere

Quantum gates manipulate qubits by rotating their Bloch vectors around specific axes:

• X gate (Pauli-X): 180° rotation around the X-axis — flips |0⟩ to |1⟩.
• Y gate (Pauli-Y): 180° rotation around the Y-axis — introduces a complex phase.
• Z gate (Pauli-Z): 180° rotation around the Z-axis — applies a phase flip.
• Hadamard (H): Rotates the qubit to an equal superposition — places it on the X-axis.
• Rx(θ), Ry(θ), Rz(θ): Arbitrary-angle rotations around X, Y, Z axes respectively.

Each gate corresponds to a unitary transformation that preserves the length of the Bloch vector. This geometric interpretation simplifies the understanding of how quantum circuits evolve over time.

Pure vs. Mixed States

The surface of the Bloch Sphere represents pure states — ideal qubit states without noise.

• Pure states: |r| = 1
• Mixed states (caused by decoherence): lie inside the sphere (|r| < 1)

Understanding this difference is key to mastering quantum error correction and noise mitigation in real-world quantum systems.

Bloch Sphere Applications in Real Quantum Systems

Bloch Sphere visualizations are widely used in:

• Quantum circuit design
• Simulations of quantum algorithms
• Quantum machine learning
• Quantum state tomography (reconstructing unknown qubit states)

Quantum computing platforms like IBM Quantum, Google Cirq, and SpinQ Cloud all make use of the Bloch Sphere in educational tools and debugging interfaces.

Common Misconceptions About the Bloch Sphere

While the Bloch Sphere is a powerful visualization tool, it's often misunderstood. Here are some frequent misconceptions:

Misconception 1: All qubits lie on the Bloch Sphere surface.

Truth: Only pure states lie on the surface. Mixed states are represented by vectors inside the sphere.

Misconception 2: You can represent multi-qubit systems using a single Bloch Sphere. Truth: The Bloch Sphere only describes single-qubit states. Multi-qubit systems require more complex representations, such as tensor products or state vectors in higher-dimensional Hilbert spaces.

Misconception 3: The Bloch Sphere shows measurement probabilities.

Truth: The Bloch Sphere shows the state of a qubit, not the outcomes of a specific measurement basis.

Understanding these limits is key to using the Bloch Sphere correctly in quantum computing education and design.

Can the Bloch Sphere Represent Entanglement?

No — the Bloch Sphere is limited to single-qubit state visualization. Entangled states, which involve correlations between two or more qubits, exist in higher-dimensional Hilbert spaces that cannot be fully captured by a single Bloch Sphere.

For example:

• The Bell state (|00⟩ + |11⟩)/√2 has no representation on an individual Bloch Sphere, because the reduced density matrix of each qubit is a completely mixed state, appearing at the center of the sphere.

To study entanglement, one must rely on tools like:

• Density matrices
• State tomography
• Entanglement entropy

Thus, while the Bloch Sphere is invaluable for visualizing isolated qubits, it cannot capture nonlocal quantum correlations fundamental to quantum computing power.

Conclusion

The Bloch Sphere is one of the most important and accessible concepts in quantum computing. By translating the complex world of quantum states into a 3D geometric model, it empowers researchers, students, and developers to build a better intuition for qubits and quantum algorithms.

Whether you're just starting in quantum computing or building real-world quantum applications, understanding the Bloch Sphere is an essential step.