Quantum Interference in Quantum Computing: 2025 Full Guide

• The core mechanism of how quantum computers operate
• What quantum interference really means in quantum computing
• How quantum interference is used in quantum computing
• And a real-world example of interference shaping computational outcomes

Let's begin by demystifying how quantum computers operate—and uncover why interference plays such a powerful role at the heart of quantum logic.

Quantum Interference in Quantum Computers: How They Actually Work

To understand how quantum interference powers quantum computing, one first needs to grasp how a quantum computer actually works. Unlike classical computers that use bits (0 or 1), quantum computers use qubits—which can exist in a superposition of both 0 and 1 at the same time.

Let's walk through the workflow of a quantum computer, focusing on the key components that make quantum interference possible.

1. Qubits and Superposition

A qubit is a quantum system, like the spin of an electron or the polarization of a photon, that can exist in a combination of two basic states:

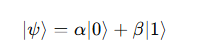
where alphaα and betaβ are complex numbers representing probability amplitudes. These amplitudes are the heart of quantum interference—because they can add or cancel out, just like waves.

To create superposition, we apply a Hadamard gate (H) to a qubit initially in state ∣0⟩, resulting in:

 

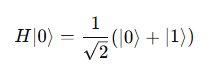
2. Quantum Gates and Phase Control

Quantum gates are like logical instructions, but they manipulate probability amplitudes and phases. Some common gates:

• Hadamard (H): Creates superpositions
• Phase (S, T, Z): Introduce relative phase shifts
• Controlled-NOT (CNOT): Creates entanglement between qubits
• Rotation gates (Rx, Ry, Rz): Rotate quantum states on the Bloch sphere

Phase control is critical because interference only happens if the phases align or misalign.

3. Interference and Quantum Parallelism

Once qubits are entangled and transformed, their probability amplitudes evolve through interference. Quantum computers don't compute in one straight line—they let all possible computational paths coexist and interact. Some paths cancel out, others reinforce—thanks to the wave-like behavior of qubits.

The final result emerges not by tracking a single path, but by shaping the landscape of probabilities through constructive and destructive interference.

Think of it this way: while classical computers "try every option one by one," quantum computers explore all options in parallel, and use interference to steer the result toward the right answer.

4. Measurement

In the final stage of a quantum computation, quantum states collapse into classical outcomes upon measurement. However, the distribution of these outcomes is not random—it is fundamentally shaped by the interference effects that have taken place throughout the quantum circuit.

For instance:

• The probability of measuring a state like ∣101⟩ may be close to zero if all computational paths leading to it have destructively interfered.
• Conversely, the likelihood of obtaining ∣011⟩ could be significantly amplified due to constructive interference among its contributing paths.

This means that quantum computers don't arrive at answers by evaluating each possibility sequentially. Instead, they exploit the wave-like nature of qubits to allow all possible computational paths to coexist and interfere—effectively shaping a probability landscape where the correct answers become the most likely outcomes.

Such interference-driven outcome shaping is what powers the advantage of quantum algorithms. For example:

• Shor's algorithm leverages interference to identify periodicities for integer factorization.
• Grover's algorithm amplifies the correct result in an unsorted database through repeated interference.
• Quantum Fourier Transform (QFT), a cornerstone of many quantum algorithms, uses interference patterns to reveal frequency components efficiently.

All of these algorithms critically depend on interference to suppress incorrect outcomes and amplify correct ones—providing exponential or quadratic speedups over their classical counterparts.

Thus, quantum interference is not merely a physical phenomenon—it is the computational engine of quantum advantage.

What is Quantum Interference in Quantum Computing?

Quantum interference refers to the phenomenon where the probability amplitudes of quantum states combine—either constructively or destructively—due to their wave-like nature.

In quantum computing, interference plays a critical role in shaping the outcome of computations.

By carefully designing quantum circuits, certain computational paths are amplified through constructive interference, while others are suppressed via destructive interference. This allows quantum algorithms to enhance the likelihood of correct answers and minimize incorrect ones, offering a fundamental advantage over classical computing.

How Is Interference Used in Quantum Computing?

Quantum interference isn't just a curious quantum phenomenon—it's a core ingredient that powers how quantum computers process and amplify useful information. Without interference, quantum computers would merely be probabilistic machines without any computational advantage.

Let's break down its role in two layers: system-wide behavior and algorithm-level design.

1. System-wide Role of Interference

In the architecture of a quantum computer, interference naturally arises from how qubits evolve and interact. When a quantum computer runs a circuit, it manipulates qubits through a series of quantum gates, causing their quantum states (or amplitudes) to interfere with one another.

Because qubit states are described by wavefunctions, they obey the rules of superposition and interference—just like ripples on a pond. Depending on how gates are arranged, quantum amplitudes may constructively interfere (increasing the chance of a certain outcome) or destructively interfere (canceling out wrong answers).

For example, in a multi-qubit system, the output is determined not by individual qubit states but by the interference pattern created by the entire quantum circuit. The success of quantum computation often hinges on carefully engineering this interference to favor correct results.

In short, interference acts as a global filter mechanism, shaping the probabilities of different outcomes and driving quantum advantage.

2. How Quantum Algorithms Harness Interference

Quantum algorithms go a step further by deliberately designing interference patterns to solve specific computational problems.

Grover's algorithm

Take Grover's algorithm as a classic example. The goal is to find a marked item from an unsorted database. Initially, all possibilities are equally probable due to superposition. But through an ingenious loop of quantum gates, the algorithm causes the amplitude of the correct answer to constructively interfere with itself, while all incorrect paths cancel each other out via destructive interference. The result? A quadratic speedup in search time.

Shor's algorithm

Similarly, Shor's algorithm uses interference to find the periodicity in number factoring problems. By encoding different paths into a quantum superposition and then applying a quantum Fourier transform, the algorithm constructs interference patterns that reveal the correct period with high probability.

These aren't accidents—quantum algorithms are precision-engineered interference machines. Their logic isn't about step-by-step calculations, but rather about shaping a wave landscape where the right answer naturally emerges from the pattern.

Real-World Example of Quantum Interference Use in a Quantum Computer

Let's take a look at a simplified version of Grover's algorithm, which demonstrates how interference is practically used.

The Problem

Suppose you want to search for a single correct item in an unsorted list of N items. Classically, this takes O(N) time. Quantumly, you can do it in O(\sqrt{N}) time.

How Interference Works Here

1. Initialization: All N states are placed into an equal superposition.

2. Oracle Step: The correct item's amplitude is flipped in phase (i.e., its sign becomes negative).

3. Amplitude Amplification: Through a series of Hadamard transforms and phase shifts, the amplitudes are manipulated such that wrong answers interfere destructively and the correct answer constructively.

4. Measurement: The correct item's amplitude is the largest—when measured, it's most likely to be observed.

This entire speed-up comes not from trying fewer possibilities, but from intelligently shaping the probability space using quantum interference. Without interference, quantum computing would just be probabilistic guessing. With interference, it becomes a precision tool, carving the correct answers out of a sea of possibilities.