Quantum Mechanical Model of the Atom: 2025 Ultimate Guide

What Is the Quantum Mechanical Model?

The quantum mechanical model is the most advanced and accurate theory of atomic structure, describing the behavior of electrons in atoms using quantum mechanics. Instead of fixed paths like in earlier models, it uses probability distributions to locate electrons in orbitals—three-dimensional regions around the nucleus.

This model revolutionized physics and chemistry by moving beyond classical laws, incorporating principles such as wave-particle duality, quantization, and uncertainty.

Key Features of the Quantum Mechanical Model

Wave-Particle Duality: Electrons exhibit both wave-like and particle-like properties. This duality is essential in understanding atomic structure.

Schrödinger Equation: The model is based on Schrödinger's time-independent wave equation, which describes the behavior of electrons as wave functions (ψ).

Atomic Orbitals: Unlike circular orbits, electrons occupy orbitals—three-dimensional probability clouds where an electron is most likely to be located.

Quantum Numbers: Four quantum numbers (n, l, m_l, m_s) define each electron's unique state in an atom, specifying energy level, orbital shape, orientation, and spin.

Heisenberg Uncertainty Principle: This principle emphasizes that we cannot precisely measure both position and momentum of an electron simultaneously—only probabilities.

What Does the Quantum Mechanical Model Explain?

The quantum mechanical model helps explain:

• Why electrons occupy discrete energy levels
• The shapes and orientations of atomic orbitals
• The electronic configuration of elements
• The origin of periodic trends (e.g., electronegativity, ionization energy)
• Chemical bonding and molecular geometry
• Spectral lines in atomic emission/absorption spectra
• Electron behavior in complex atoms beyond hydrogen

It is a foundation for fields like quantum chemistry, semiconductor physics, and quantum computing.

Who Developed the Quantum Mechanical Model?

The development of the quantum mechanical model was a collaborative achievement:

Quantum Mechanical Model Formula: The Schrödinger Equation

At the heart of the model is the time-independent Schrödinger equation:

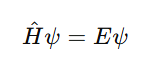
Where:

• H^is the Hamiltonian operator (total energy)
• ψ is the wave function of the system
• E is the energy eigenvalue

Solving this equation for the hydrogen atom yields the atomic orbitals—s, p, d, f—each corresponding to different energy and shape distributions.

Quantum Numbers in the Model

Every electron in an atom is described by four quantum numbers:

Principal quantum number (n): Energy level (shell)

Azimuthal quantum number (l): Orbital shape (s=0, p=1, d=2, f=3)

Magnetic quantum number (mₗ): Orbital orientation

Spin quantum number (mₛ): Electron spin direction (+½ or –½)

These numbers uniquely define the electron's probable location.

Applications in Atomic and Molecular Systems

The quantum mechanical model enables deep insights into the structure and behavior of real atomic and molecular systems:

1. Hydrogen Atom

Schrödinger's equation can be solved exactly for hydrogen.

Predicts quantized energy levels and spherical s-orbitals.

Matches experimental spectral data with high precision.

2. Helium Atom

Involves electron-electron repulsion, requiring approximation methods like Hartree-Fock or Density Functional Theory (DFT).

Demonstrates the model's flexibility in multi-electron atoms.

3. Molecular Orbitals

Quantum mechanics underpins Molecular Orbital Theory, predicting bonding and anti-bonding interactions.

Used in computational chemistry to simulate reaction pathways, activation energies, and transition states.

4. Periodic Table Structure

Explains atomic trends like ionization energy and atomic radius using electron configurations derived from quantum principles (e.g., Aufbau principle, Pauli exclusion, and Hund's rule).

5. Quantum Dots and Nanotechnology

The model explains electron confinement in nanoscale materials.

Used to design quantum wells, lasers, and nanosensors based on electron tunneling and discrete energy levels.

Broader Scientific and Technological Applications

Beyond atoms and molecules, the quantum mechanical model forms the theoretical basis of multiple modern scientific and industrial fields:

1. Chemistry

Explains chemical bonding, molecular shapes (via Valence Shell Electron Pair Repulsion theory, or VSEPR), and spectroscopic behavior.

2. Physics

Fundamental to quantum field theory, particle physics, and solid-state physics.

Explains phenomena like quantum tunneling, spin, and magnetism.

3. Material Science

Enables design of semiconductors, superconductors, and nanomaterials.

Essential in the analysis of band structures, defects, and optical properties.

4. Quantum Computing

Qubits, superposition, and entanglement are direct applications of quantum principles.

Quantum gates and error correction rely on the quantum mechanical behavior of particles.

5. Emerging Fields

Quantum cryptography, atomic clocks, spintronics, and quantum sensors all build on this model's foundational insights.

Quantum Mechanical Model in Education and Research

The quantum mechanical model is a core part of:

• High school chemistry (usually introduced after Bohr model)
• University-level quantum physics and physical chemistry
• Quantum computing and nanotechnology training

Modern tools like SpinQ's educational quantum computers allow hands-on interaction with quantum states, bridging abstract quantum theory with real-world applications.

Quantum Mechanical Model vs Bohr Model

Why the Quantum Mechanical Model Replaced the Bohr Model

The Bohr model introduced the idea of quantized energy levels but failed to explain the complexities of multi-electron atoms and electron behavior under magnetic or electric fields. The quantum mechanical model improved upon this by:

• Treating electrons as wave functions instead of particles in orbit.
• Accounting for the uncertainty principle, which states that the exact position and momentum of an electron cannot be known simultaneously.
• Using atomic orbitals (s, p, d, f) to define electron probability regions.

Conclusion: Why the Quantum Mechanical Model Matters

The quantum mechanical model of the atom is a cornerstone of modern science. It replaced outdated atomic models with a framework that accurately describes atomic structure, chemical behavior, and electronic properties.

Whether you're exploring atomic spectra, chemical bonding, or quantum computing, this model is your starting point.

FAQs

Is the Quantum Mechanical Model Only for Atoms?

While most educational contexts refer to the quantum mechanical model of the atom, the model itself is a general framework in quantum mechanics. It is used to describe not just atoms, but also:

• Molecules (via quantum chemistry)
• Solids and semiconductors (via solid-state physics)
• Photons, electrons, and other particles in quantum field theory

However, the atom-based version is the most widely taught and understood application, especially in chemistry and physics education.

Why Is the Quantum Mechanical Model More Accurate?

Compared to earlier models like Bohr's, the quantum mechanical model:

• Applies to multi-electron atoms
• Explains electron repulsion and shielding effects
• Incorporates wave-particle duality of electrons
• Uses quantum numbers to define energy levels and orbital shapes
• Predicts atomic behavior under external electric and magnetic fields

This makes it not only more precise for hydrogen but also universally applicable.